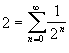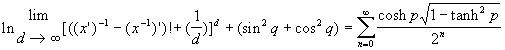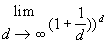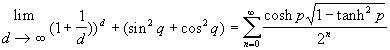| Jedem angehenden Wirtschaftinformatiker wird schon zu Beginn seines Studiums beigebracht, z.B.
die Summe zweier Größen nicht etwa in der nebenstehenden Form (1) darzustellen ist. |
(1) |
1+1=2 |
| Diese Form ist banal und zeugt von schlechtem Stil. Schon mathematische Analphabeten wissen nämlich, dass |
(2) |
1=ln(e) |
| und weiterhin, dass gilt: |
(3) |
1=sin2q+cos2q |
| Außerdem ist für den kundigen Leser offensichtlich, dass gilt: |
(4) |
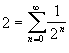 |
| Daher kann Gleichung (1) viel wissenschaftlicher ausgedrückt werden in Form |
(5) |
| ln(e) + (sin2q + cos2q) = |
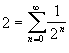 |
|
| Es ist sofort einzusehen, dass |
(6) |
1 = coshp |
| und wegen (7) kann die Gleichung (5) in folgender Weise
zu (8) vereinfacht werden: |
(7) |
| e = |
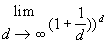 |
|
| |
(8) ln |
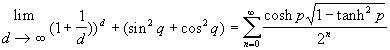 |
|
| Wenn wir berücksichtigen, dass |
(9) |
0!=1 |
|
und uns erinnern, dass die Inverse einer transponierten Matrix die Transponierte der
Inversen ist, können wir unter der Restriktion eines eindimensionalen Raumes eine weitere
Vereinfachung durch die Einführung des Vektors x erzielen, wobei:
|
(10) |
(x')-1 - (x-1)' = 0 |
| Kombinieren wir Gleichung 9 und Gleichung 10, so ergibt sich: |
(11) |
((x')-1 - (x-1)')! = 1 |
Eingesetzt in Gleichung 8 reduziert sich unser Ausdruck zu folgender trivialen Form:
Spätestens jetzt ist es offensichtlich, dass die Gleichung 12 viel klarer und leichter
zu verstehen ist als Gleichung 1. Wird die Logik des angehenden Wirtschaftsinformatiker
bald durch die hier verwandten einfachen Prinzipien bestimmt, so lassen sich alle
mathematischen Probleme klar und deutlich lösen.
gezeichnet. Ein verzweifelter WiInf, der den roten Faden in der Mathe I - Vorlesung
WS 95/96 bei Herrn Priv.-Doz. Dr. Hans-Georg Rück verloren hat.